磁盘结构
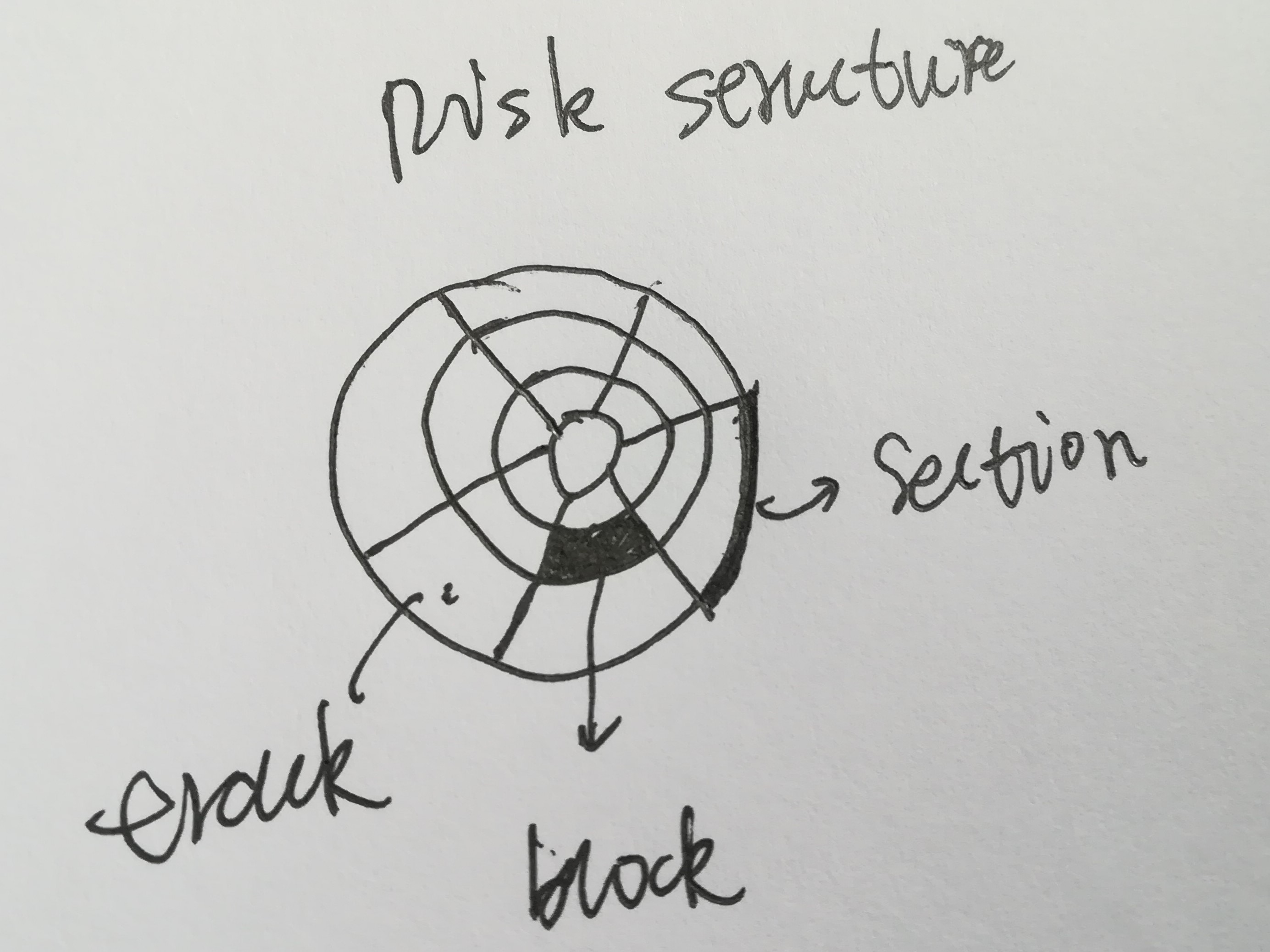
按照顺时针方向,一个盘片由很多section组成,编号0-N。从里向外分,又由多个track组成,编号0-N,section和track交叉的地方叫做block,所以一个block可以由section和track来定位。每一个block的大小是一样的。
操作系统读取数据都是按照block为单位进行。
在block内,数据的存储结构可以看成一个一维数组,大致结构是这样(假设一个block的size为512byte)

Disk的读写头可以旋转和伸缩来定位一个block
为了使磁盘中的数据可以被应用程序使用,必须先copy数据到随机读写存储器RAM中,而这正是耗时的操作。
磁盘如何存储数据库数据
假设现在有一个Employee表,其中有一些字段,如下所示,所以一行数据的大小是128byte

假设总共有100行这样的数据

所以每一个block可以存储4行这样的数据,这100行数据需要25个block,假设现在按照这样的方式来查询一条记录,最多需要查找25个block.
那索引为什么可以减少查找的次数呢?
什么是索引
我们建一个简单的索引,有两个字段,一个eid,表示employee的id,还有一个字段pointer,指向数据存储在disk上的位置。empolyee中的每一行,在index上都有一条记录

当然我们也需要考虑如何存储这个索引表。如果索引存放在disk上,那么这个索引需要占据多少个block呢?eid大小为10bytes,pointer大小为6bytes,所以一行索引就有16个bytes大小。100条索引就需要占据100 * 16 / 512,也就是 4个block
在现在的情况下,我们查找employee表中的一条数据,最多就只需要4次索引表查找和一次employee表读取,相比没有索引的情况效率提升了很多
多级索引
如果现在把employee表中的数据行数增加到1000行,那么同理,数据表需要250个block,索引表需要40个block,现在查询一条记录就最多需要41次block的读取和拷贝(IO)
根据建立索引可以减少查找次数的理论,我们现在可以建立二级索引,也就是对上面的一级索引再建立索引,二级索引存储一级索引所在的block,现在一级索引占用40个block,所以二级索引表有40条记录,每一个索引记录大小为16byte,所以二级索引占用的block为40*16/512,也就是2个block。那么现在再来根据二级索引查找到一级索引所在的block,再根据一级索引直接定位到employee表中的某条数据所在的block,最多一共需要2+1+1=4次查找(IO),相比之前效率又提升了不少。
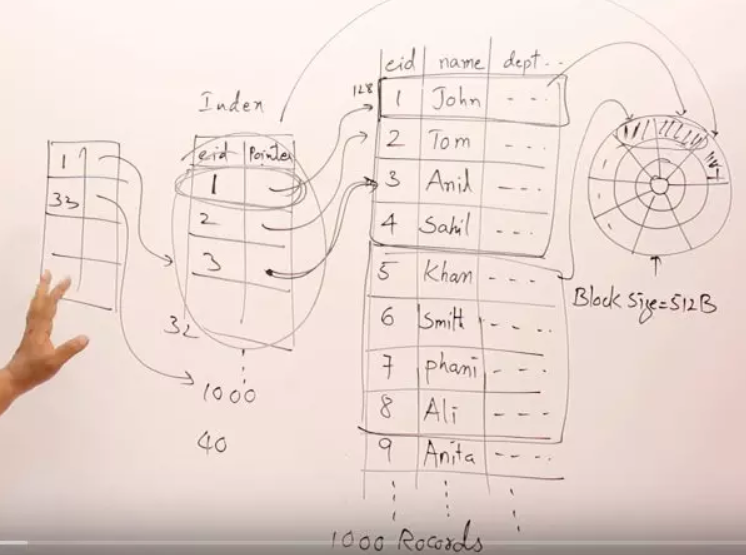
随着数据表中数据记录的增加,可以建立三级,四级….索引来减少IO次数
多路(n-way)搜索树
二叉搜索树
每个节点只有一个值,一个节点最多两个子节点,左子节点比父节点小,右子节点比父节点大
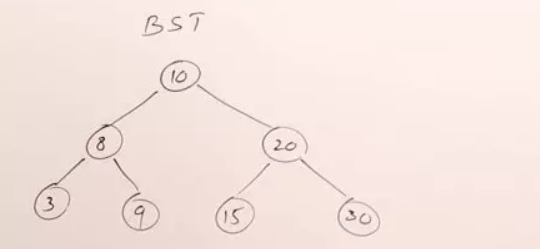
一颗树代表了某一级索引,搜索树的高度(深度)代表了最多IO的次数,所以减少树的高度可以减少IO的次数
思路就是一个节点存储多个值,相应的子节点最大个数也可以有多个
n-way搜索树
由二叉搜索树扩展,让每个节点最多可以存n-1个索引值,每个节点可以有n个子节点,就是n-way搜索树
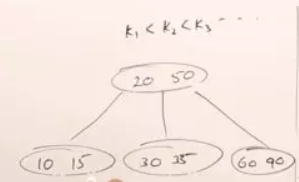
上面就是一个3路搜索树
我们可以使用这样的数据结构来作为索引,但是n-way搜索树也存在一些问题
比如现在有三个数据:10,20,30,要用一个10-way搜索树来构建。很有可能,最终会构建出一个这样的树

这是一种最坏的情况,相当于退化成链表结构。
B树:多路搜索树上增加限制
B树,实际上可以看作是n-way搜索树 + 规则(如何构建这棵树的规则)
规则:
- 每个节点至少有
[n/2]个子节点 - 根节点可以最少有
2个子节点 - 所有的叶子节点必须在一个层级
- 创建过程是由下往上的
值:10,20,40,50。要构建一个4-way搜索树。4-way搜索树,意味着一个节点最多可以有3个值。
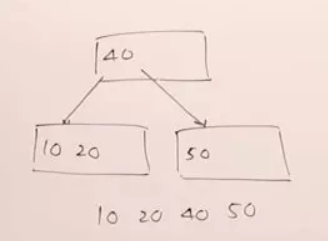
继续插入操作,最后形成的结果是:

每一个节点可以有多个值,每个值里面包含一个键和位置指针,键用来作为标识,数据值标识数据存放的位置
B+树
在B+树中,不是每个值旁边都有一个指向数据存储位置的指针,只有叶子节点才有。非叶子节点的值,在叶子节点上有他的副本
