二叉查找树，二叉平衡树

Java集合TreeMap和TreeSet中底层使用了红黑树，集合HashMap在JDK1.8 使用了数组+链表+红黑树的数据结构

那么到底什么是红黑树呢，上数据结构课程的时候只是学到了二叉查找树(Binery Search Tree,BST)的概念，简单介绍过平衡树。

现在再来看一下什么是二叉查找树和平衡树

二叉查找树

二叉查找树又称二叉排序树

二叉查找树的特点

排序二叉树是一种特殊结构的二叉树，可以非常方便地对树中所有节点进行排序和检索。

排序二叉树要么是一棵空二叉树，要么是具有下列性质的二叉树：

• 若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
• 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
• 它的左、右子树也分别为排序二叉树

二叉排序树的结构如下：

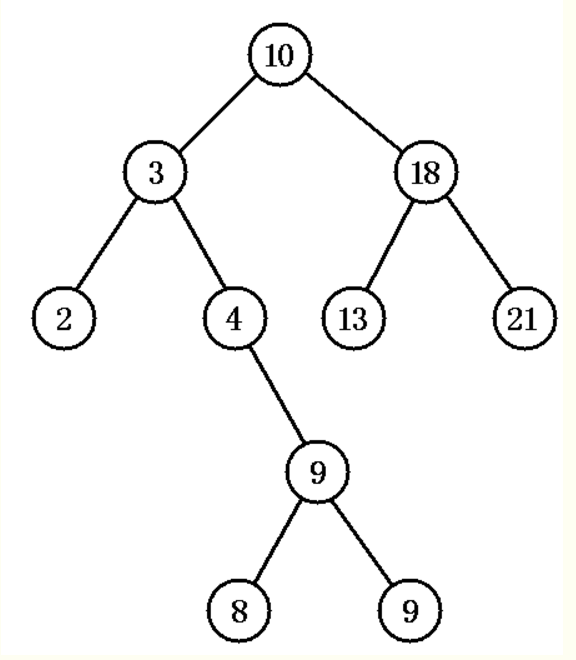
按照这种方式来进行查找，正是二分查找的思想，查找所需的最大次数等于二叉查找树的高度。插入节点的时候也是一层一层比较，然后找到合适的位置插入

二叉查找树缺点

但是，二叉查找树也有自身的缺点

例如：假设初始的二叉查找树只有三个节点，根节点值为9，左孩子值为8，右孩子值为12

接下来我们依次插入如下五个节点：7,6,5,4,3。依照二叉查找树的特性，结果会变成什么样呢？

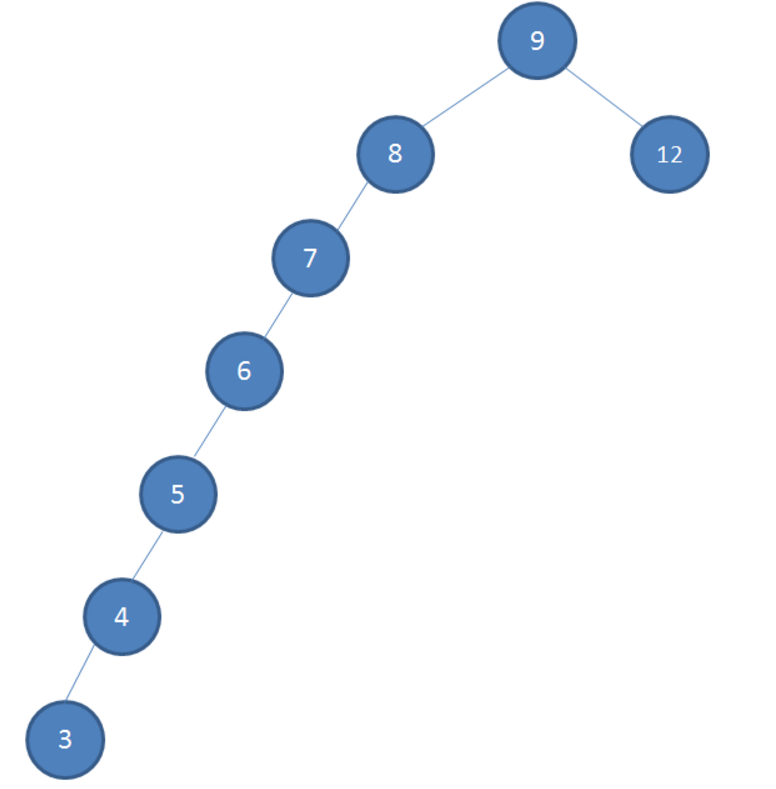
如此一来，查找就变成了线性查找，查找的效率大大降低

那么如何解决新节点的插入导致二叉查找树不平衡呢，这就引入了平衡树的概念

二叉平衡树

平衡二叉树：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。构造与调整方法 平衡二叉树的常用算法有红黑树、AVL、Treap等

红黑树

红黑树是一种自平衡的二叉查找树，除了具有二叉查找树的特点外，还具有以下特性：

• 节点是红色或者黑色
• 根节点是黑色
• 每个叶节点都是红色的空节点
• 每个红色节点的两个子节点都是黑色
• 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

下面就是一颗红黑树

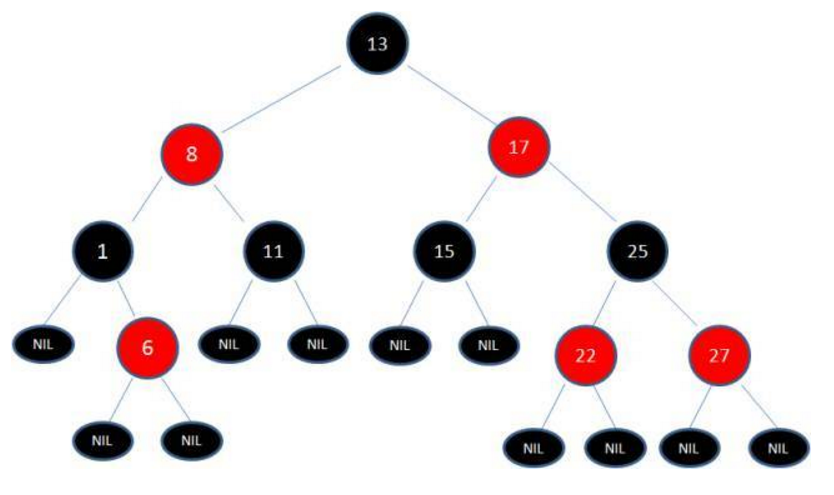
由此我们可以得出结论：对于给定的黑色高度为 N 的红黑树，从根到叶子节点的最短路径长度为 N-1，最长路径长度为 2 * (N-1)

• 红黑树通过上面这种限制来保证它大致是平衡的——因为红黑树的高度不会无限增高，这样保证红黑树在最坏情况下都是高效的，不会出现普通排序二叉树的情况。
• 由于红黑树只是一个特殊的排序二叉树，因此对红黑树上的只读操作与普通排序二叉树上的只读操作完全相同，只是红黑树保持了大致平衡，因此检索性能比排序二叉树要好很多。
• 但在红黑树上进行插入操作和删除操作会导致树不再符合红黑树的特征，因此插入操作和删除操作都需要进行一定的维护，以保证插入节点、删除节点后的树依然是红黑树